It is straightforward to determine the polarity of the woofer in a hybrid electrostatic system. Usually the woofer is marked either with a plus sign or a red dot on one terminal; I don't know how universal the convention is, but in my experience this mark means that if you apply a positive voltage to this terminal relative to the second terminal, the woofer will move in the forward direction towards the listener. It is easy to verify that this is the case by connecting a battery through a suitable current limiting resistor to the woofer, and you can observe which way it moves.

With ESLs the situation is not quite so clear. First of all, we usually drive ESLs through step-up transformers and you cannot apply a DC voltage through a transformer. Even if you could, it is not so easy to observe the diaphragm motion since it is obscured by the surrounding stators.

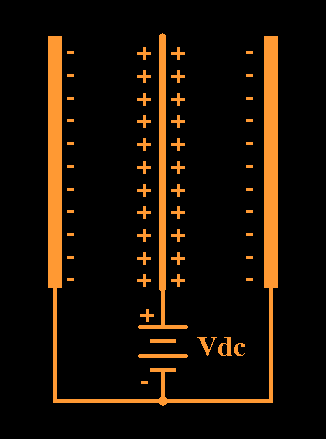
However, it is not too difficult to figure out which way the ESL should move from first principles, at least for relatively low frequencies. The first diagram shows an ESL biased such that the diaphragm is made positive with respect to the stators; this is the way I bias my ESLs. If everything is symmetrical, the diaphragm will be equally attracted to each stator so that it will remain at the midpoint between the stators.

Now imagine what happens when an AC signal is superimposed upon this DC bias, as shown in the second figure. Assume that the instantaneous polarity of the AC signal is as shown, with the stator on the left made positive with respect to the stator on the right. The applied signal will re-distribute the charge on the stators; the left-hand stator will be made somewhat less negative, and the right-hand stator will be somewhat more negative with respect to the diaphragm in the middle. This has been indicated by the migration of some of the negative charge from the left stator over to the right one. Note however that the positive charge on the diaphragm has remained the same, indicating that the diaphragm is operated in constant-charge mode.

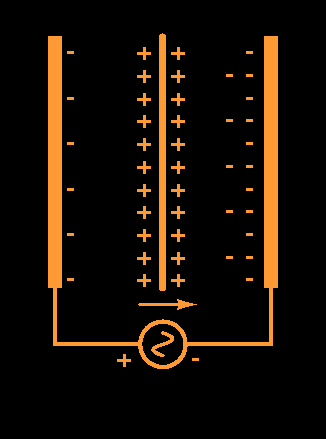
The fact that the left stator is now less negative (or equivalently, more positive) with respect to the diaphragm means that the left stator will attract the diaphragm less than it did in the DC biased condition. Similarly, the fact that the right-hand stator is now more negative with respect to the diaphragm, means that the right stator will attract the diaphragm more than it did in the DC biased condition. Therefore, the diaphragm will move to the right, as indicated by the arrow in the figure.

Of course, the diaphragm could be DC biased negatively with respect to the stators instead of positively. In that case, for the given polarity of AC signal the diaphragm would move toward the left instead of toward the right. (You also need to be careful about the step-up transformer that is used to drive the ESLs; sometimes the transformer can introduce an unexpected inversion of the AC signal).

But there are really two issues about polarity; one question is how to achieve a particular polarity, which I hopefully have addressed in the above discussion. But there is also the question as to what the ESL polarity should be with respect to the polarity of the woofer in the system. Unfortunately, this question is not so straightforward to resolve. I am using third-order Butterworth filters in my hybrid electrostatic system. The theory of these filters says that if you apply the input signals in phase to the lowpass and highpass filters, the combined output should have constant amplitude throughout the crossover region. However, I have found that I can achieve the best response if I invert the polarities of the signals (I also have to shift the position of the ESL relative to the woofer to achieve this). The reason is that the ESL and woofer drivers exhibit phase shifts of their own, which are frequency dependent. The problem is rather complex and you really need something like an FFT measurement system to see what is happening.